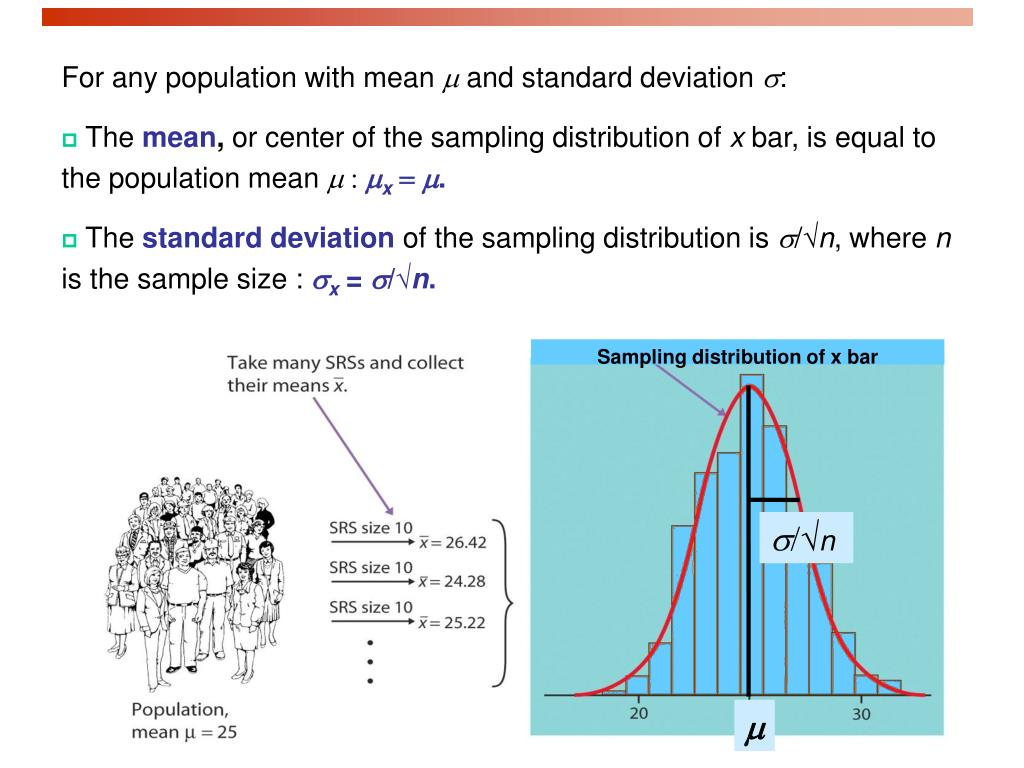
Standard Deviation Means Sampling Distribution . the standard deviation of the sampling distribution is smaller than the standard deviation of the population. describe the distribution of the sample mean. if we obtain a random sample and calculate a sample statistic from that sample, the sample statistic is a random variable (wow!). the standard deviation of the sampling distribution is smaller than the standard deviation of the population. Solve probability problems involving the distribution of the sample mean. \(\overline{x}\), the mean of the measurements in a sample of size \(n\); the sample mean is a random variable and as a random variable, the sample mean has a probability. this distribution of sample means is known as the sampling distribution of the mean and has the following properties: The distribution of \(\overline{x}\) is its. In the examples so far, we were given the population.
from www.slideserve.com
this distribution of sample means is known as the sampling distribution of the mean and has the following properties: The distribution of \(\overline{x}\) is its. In the examples so far, we were given the population. if we obtain a random sample and calculate a sample statistic from that sample, the sample statistic is a random variable (wow!). describe the distribution of the sample mean. the sample mean is a random variable and as a random variable, the sample mean has a probability. Solve probability problems involving the distribution of the sample mean. the standard deviation of the sampling distribution is smaller than the standard deviation of the population. \(\overline{x}\), the mean of the measurements in a sample of size \(n\); the standard deviation of the sampling distribution is smaller than the standard deviation of the population.
PPT Sampling distributions for sample means PowerPoint Presentation
Standard Deviation Means Sampling Distribution describe the distribution of the sample mean. describe the distribution of the sample mean. the standard deviation of the sampling distribution is smaller than the standard deviation of the population. the sample mean is a random variable and as a random variable, the sample mean has a probability. \(\overline{x}\), the mean of the measurements in a sample of size \(n\); this distribution of sample means is known as the sampling distribution of the mean and has the following properties: The distribution of \(\overline{x}\) is its. the standard deviation of the sampling distribution is smaller than the standard deviation of the population. In the examples so far, we were given the population. if we obtain a random sample and calculate a sample statistic from that sample, the sample statistic is a random variable (wow!). Solve probability problems involving the distribution of the sample mean.
From www.slideserve.com
PPT 7.0 Sampling and Sampling Distribution PowerPoint Presentation Standard Deviation Means Sampling Distribution \(\overline{x}\), the mean of the measurements in a sample of size \(n\); the standard deviation of the sampling distribution is smaller than the standard deviation of the population. In the examples so far, we were given the population. the sample mean is a random variable and as a random variable, the sample mean has a probability. . Standard Deviation Means Sampling Distribution.
From www.studypool.com
SOLUTION Statistics and probability mean variance and standard Standard Deviation Means Sampling Distribution the standard deviation of the sampling distribution is smaller than the standard deviation of the population. if we obtain a random sample and calculate a sample statistic from that sample, the sample statistic is a random variable (wow!). the standard deviation of the sampling distribution is smaller than the standard deviation of the population. this distribution. Standard Deviation Means Sampling Distribution.
From www.slideserve.com
PPT Chapter 12 Sampling Distributions PowerPoint Presentation, free Standard Deviation Means Sampling Distribution this distribution of sample means is known as the sampling distribution of the mean and has the following properties: describe the distribution of the sample mean. if we obtain a random sample and calculate a sample statistic from that sample, the sample statistic is a random variable (wow!). The distribution of \(\overline{x}\) is its. the standard. Standard Deviation Means Sampling Distribution.
From www.slideserve.com
PPT Sampling distributions for sample means PowerPoint Presentation Standard Deviation Means Sampling Distribution the sample mean is a random variable and as a random variable, the sample mean has a probability. The distribution of \(\overline{x}\) is its. the standard deviation of the sampling distribution is smaller than the standard deviation of the population. if we obtain a random sample and calculate a sample statistic from that sample, the sample statistic. Standard Deviation Means Sampling Distribution.
From www.youtube.com
Statistics Mean and Standard Deviation of a Sampling Distribution Standard Deviation Means Sampling Distribution In the examples so far, we were given the population. the sample mean is a random variable and as a random variable, the sample mean has a probability. \(\overline{x}\), the mean of the measurements in a sample of size \(n\); describe the distribution of the sample mean. this distribution of sample means is known as the. Standard Deviation Means Sampling Distribution.
From www.slideserve.com
PPT Sampling Distribution of the Mean PowerPoint Presentation, free Standard Deviation Means Sampling Distribution if we obtain a random sample and calculate a sample statistic from that sample, the sample statistic is a random variable (wow!). In the examples so far, we were given the population. describe the distribution of the sample mean. the sample mean is a random variable and as a random variable, the sample mean has a probability.. Standard Deviation Means Sampling Distribution.
From curvebreakerstestprep.com
Standard Deviation Variation from the Mean Curvebreakers Standard Deviation Means Sampling Distribution this distribution of sample means is known as the sampling distribution of the mean and has the following properties: describe the distribution of the sample mean. if we obtain a random sample and calculate a sample statistic from that sample, the sample statistic is a random variable (wow!). the standard deviation of the sampling distribution is. Standard Deviation Means Sampling Distribution.
From mavink.com
Standard Deviation Chart Standard Deviation Means Sampling Distribution The distribution of \(\overline{x}\) is its. the standard deviation of the sampling distribution is smaller than the standard deviation of the population. the standard deviation of the sampling distribution is smaller than the standard deviation of the population. this distribution of sample means is known as the sampling distribution of the mean and has the following properties:. Standard Deviation Means Sampling Distribution.
From www.numerade.com
SOLVED Given the following sampling distribution of one mean with Standard Deviation Means Sampling Distribution the standard deviation of the sampling distribution is smaller than the standard deviation of the population. describe the distribution of the sample mean. In the examples so far, we were given the population. The distribution of \(\overline{x}\) is its. \(\overline{x}\), the mean of the measurements in a sample of size \(n\); this distribution of sample means. Standard Deviation Means Sampling Distribution.
From saylordotorg.github.io
The Sampling Distribution of the Sample Mean Standard Deviation Means Sampling Distribution the sample mean is a random variable and as a random variable, the sample mean has a probability. the standard deviation of the sampling distribution is smaller than the standard deviation of the population. The distribution of \(\overline{x}\) is its. describe the distribution of the sample mean. In the examples so far, we were given the population.. Standard Deviation Means Sampling Distribution.
From demonstrations.wolfram.com
Sampling Distribution of the Mean and Standard Deviation in Various Standard Deviation Means Sampling Distribution the sample mean is a random variable and as a random variable, the sample mean has a probability. In the examples so far, we were given the population. the standard deviation of the sampling distribution is smaller than the standard deviation of the population. describe the distribution of the sample mean. \(\overline{x}\), the mean of the. Standard Deviation Means Sampling Distribution.
From www.slideserve.com
PPT SAMPLING AND SAMPLING DISTRIBUTIONS PowerPoint Presentation, free Standard Deviation Means Sampling Distribution Solve probability problems involving the distribution of the sample mean. the standard deviation of the sampling distribution is smaller than the standard deviation of the population. the standard deviation of the sampling distribution is smaller than the standard deviation of the population. The distribution of \(\overline{x}\) is its. In the examples so far, we were given the population.. Standard Deviation Means Sampling Distribution.
From slidetodoc.com
Chapter 7 Sampling Distributions Section 7 3 Sample Standard Deviation Means Sampling Distribution the standard deviation of the sampling distribution is smaller than the standard deviation of the population. In the examples so far, we were given the population. Solve probability problems involving the distribution of the sample mean. The distribution of \(\overline{x}\) is its. this distribution of sample means is known as the sampling distribution of the mean and has. Standard Deviation Means Sampling Distribution.
From articles.outlier.org
Understanding Sampling Distributions What Are They and How Do They Standard Deviation Means Sampling Distribution The distribution of \(\overline{x}\) is its. this distribution of sample means is known as the sampling distribution of the mean and has the following properties: if we obtain a random sample and calculate a sample statistic from that sample, the sample statistic is a random variable (wow!). describe the distribution of the sample mean. the standard. Standard Deviation Means Sampling Distribution.
From www1.udel.edu
Public Management Statistics Class 24 Notes Standard Deviation Means Sampling Distribution the standard deviation of the sampling distribution is smaller than the standard deviation of the population. if we obtain a random sample and calculate a sample statistic from that sample, the sample statistic is a random variable (wow!). In the examples so far, we were given the population. the sample mean is a random variable and as. Standard Deviation Means Sampling Distribution.
From www.scribbr.com
The Standard Normal Distribution Examples, Explanations, Uses Standard Deviation Means Sampling Distribution this distribution of sample means is known as the sampling distribution of the mean and has the following properties: the standard deviation of the sampling distribution is smaller than the standard deviation of the population. Solve probability problems involving the distribution of the sample mean. The distribution of \(\overline{x}\) is its. \(\overline{x}\), the mean of the measurements. Standard Deviation Means Sampling Distribution.
From www.slideserve.com
PPT Chapter 5 Sampling Distributions PowerPoint Presentation, free Standard Deviation Means Sampling Distribution In the examples so far, we were given the population. describe the distribution of the sample mean. if we obtain a random sample and calculate a sample statistic from that sample, the sample statistic is a random variable (wow!). Solve probability problems involving the distribution of the sample mean. \(\overline{x}\), the mean of the measurements in a. Standard Deviation Means Sampling Distribution.
From www.scribd.com
Sampling Distribution PDF Standard Deviation Mean Standard Deviation Means Sampling Distribution the standard deviation of the sampling distribution is smaller than the standard deviation of the population. Solve probability problems involving the distribution of the sample mean. In the examples so far, we were given the population. if we obtain a random sample and calculate a sample statistic from that sample, the sample statistic is a random variable (wow!).. Standard Deviation Means Sampling Distribution.